written before
In programming, we often need to use a group of data elements of the same type as a whole. We need to create such element groups, use variables to record them or pass in functions, etc., "linear table" It is an abstraction of such a group of elements. It is a collection of elements of a certain type and records a sequential relationship between elements. It is one of the most basic data structures and is widely used in practical programs, such as list and tuple in Python. All can be seen as an implementation of a linear table.
Based on comprehensive consideration of various practical operations, we propose two forms of implementing linear tables: "sequential list" and "linked list".
"Sequence table" is to store the order of elements in the table in a large continuous storage interval, so the order of elements here is represented by their storage order. "Linked list" stores the elements in the list in a series of nodes (the storage location of the nodes can be continuous or discontinuous, which means that they can exist in any unoccupied memory location), These nodes are constructed by connection, and the nodes are divided into "data field" and "pointer field". The "single linked list" we are going to learn this time is an implementation form of "linked list".

Before I officially say "single linked list", let me talk about two things that many people are foolishly confused about at the beginning of learning linked list: "head node" and "head pointer".
The establishment of the "head node" is for the unity and convenience of operation. It is placed before the node of the first element. Its data field is generally meaningless, and it is not necessary for the linked list itself. What is the purpose of setting up the head node? In fact, it is to operate the linked list more conveniently at certain times. With the head node, when we insert or delete a node before the first element, its operation is unified with the operation of other nodes. .
"Head pointer", as the name implies, is a pointer to the first node of the linked list. If there is a head node, then it is a pointer to the head node. It is a necessary element of the linked list and no matter whether the linked list is empty or not, the head pointer cannot be empty, because when you access the linked list, you always have to know where it is, so that you can find the position of the next node through its pointer field. That is to say, knowing the head pointer, we can access the elements of the entire linked list, so it must exist, which is what we often call "identity", which is why we generally use the head pointer to represent the linked list.
Single list
N nodes are linked to form a linked list, which is also called "chained storage structure" in books. Because each node in this linked list contains only one pointer field, it is also called "single linked list". The singly linked list links the data elements of the linear list together in their logical order through the pointer field of each node. The storage location of the first node of the singly linked list is called "head pointer", and the pointer of the last node is "null", which is generally represented by "^".

The above figure is a singly linked list without a head node. Let's take a look at a singly linked list with a head node:

There is also an empty linked list:
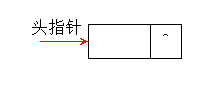
Through the above three figures, we find that no matter whether the singly linked list is empty or not, whether there is a head node or not, the head pointer exists. Whether the linked list is empty, the head pointer cannot be empty".
In order to facilitate subsequent operations, we generally define a simple node class first:
class Node(object): def __init__(self,data): self.data = data self.next = None
Basic operations of a singly linked list
First, let's create a linked list class:
class LinkList(object): def __init__(self): self.head = Node(None) # Determine if the linked list is empty def IsEmpty(self): p = self.head # Head pointer if p.next == None: print( "List is Empty") return True return False # print linked list def PrintList(self): if self.IsEmpty(): return False p = self.head while p: print(p.data,end=' ') p = p .next
1. Create a singly linked list
The process of creating a singly linked list is actually a process of dynamically generating a linked list. To put it simply, it starts from an "empty linked list", establishes the nodes of each element in turn, and inserts them into the linked list one by one. The time complexity is O(n):
def InitList(self,data): self.head = Node(data[0]) # head node p = self.head # head pointer for i in data[1:]: node = Node(i) p.next = node p = p.next
Let's test it:
# testlst = LinkList()data = [1, 4, 5, 8, 2, 3]lst.InitList(data)lst.PrintList()
The output is as follows:
1 4 5 8 2 3
2. Calculate the length of a singly linked list
When using a linked list, we often need to find the length of the table. For this reason, we can create a function with the length of the ball table. This function scans from left to right, traverses all nodes in the table and completes the count. The time complexity is O (n):
def LengthList(self): if self.IsEmpty(): return 0 p = self.head cnt = 0 while p: cnt += 1 p = p.next return cnt
Let's test it:
# testlst = LinkList()data = [1, 4, 5, 8, 2, 3]lst.InitList(data)print(lst.LengthList())
The output is as follows:
6
3. Insertion of a singly linked list
Suppose we want to insert node s after node p, we only need to insert node s between node p and node p.next. It is easy to say, so how to insert it? Please see the picture below:
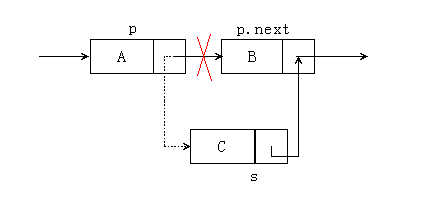
As can be seen from the above figure, the insertion of a singly linked list node does not need to alert other nodes at all, only the pointers of s.next and p.next need to be changed slightly. Let the successor of p be the successor of s, and then change the successor of s into the successor of p. It must be remembered here that the order of insertion operations cannot be changed. As for why, you can pick up a pen and paper and draw it manually, and the result will come out at once (for the special case of the header and footer of a singly linked list, the operation is the same ).
# Insertion of a singly linked list (insert data after the s-th node) def InsertList(self,s,data): if self.IsEmpty() or s self.LengthList(): print("Insert failed!") return p = self.head index = 1 while index
Let's test it:
# testlst = LinkList()data = [1, 4, 5, 8, 2, 3]lst.InitList(data)lst.InsertList(0,666)lst.PrintList()
The output is as follows:
1 666 4 5 8 2 3
4. Singly linked list deletion
After reading the insertion, let's now look at the deletion of the singly linked list. Suppose we want to delete a node q, in fact, it is to bypass the pointer of its predecessor node p, and directly point to the successor node of q, as shown in the following figure:
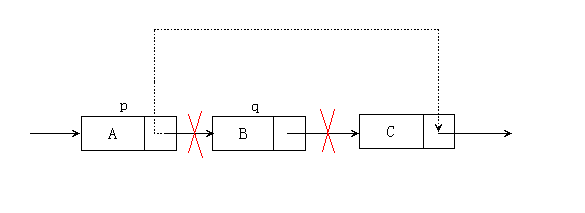
As can be seen from the above figure, we only need one step to implement the delete operation, that is, let p.next be directly the next of p's next, and p's next to be q, so that is p.next = q.next, the time is complicated The degree is O(n).
# Deletion of a singly linked list (delete the s-th node) def DeleteList(self, s): if self.IsEmpty() or s self.LengthList(): print("Delete failed! ") return p = self.head index = 1 while index
It can be seen from p = None that in Python, simply assigning the pointer to None will discard the original node of the linked list, and the storage management system of the Python interpreter will automatically reclaim unused storage.
Let's test it:
# testlst = LinkList()data = [1, 4, 5, 8, 2, 3]lst.InitList(data)lst.DeleteList(3)lst.PrintList()
The output is as follows:
1 4 8 2 3
5. Reading a singly linked list
In the sequential structure, it is very easy for us to obtain the storage location of any element, but in the singly linked list, we have no way of knowing where the i-th element is at the beginning, so we can only find it silly from the beginning, so The operation of obtaining the i-th element of a singly linked list is relatively troublesome in algorithm.
# Read the singly linked list (get the value of the s-th node) def GetList(self, s): if self.IsEmpty() or s self.LengthList(): print("Read failed! ") return p = self .head index = 1 while index
From the above code, we can clearly see that to get the i-th element of a singly linked list is to search from the beginning until the i-th element is known, so we can easily estimate its time complexity to be O(n). Nothing is perfect. There are good places and bad places. The reading of elements is one of the shortcomings of singly linked lists.
written after
There are actually many operations on the singly linked list. I just wrote a few commonly used ones. I hope you can try it yourself and understand them thoroughly. When you encounter such a problem, which aspect to think about and how to do it is the most important. Only by learning these, you will know how to start when you encounter related problems in the future.
Most of the diagrams I have given in the explanation of each operation above are clear from the diagrams. The algorithm is actually like this. Do the following with more hands-on. If you don't understand it, just draw it by hand, and draw and draw the idea.
Finally, let's summarize the time complexity of linked list operations. If you don't know how to estimate the time complexity of the algorithm, please see my step-by-step guide to learn the time complexity and space complexity.
Creating an empty table O(1).
Creating a singly linked list O(n)
Inserting elements: head insertion is O(1); tail insertion is O(n), because the last node of the table is also found; positioning insertion is O(n).
Deleting elements: O(1) for head deletion; O(n) for tail deletion, for the same reasons; O(n) for positioning deletion.
Here is a summary of the code for all of the above operations:
# Node class class Node(object): def __init__(self,data): self.data = data self.next = None# Linked list class LinkList(object): def __init__(self): self.head = Node(None ) # Determine if the linked list is empty def IsEmpty(self): p = self.head # Head pointer if p.next == None: print("List is Empty") return True return False # Print the linked list def PrintList(self): if self.IsEmpty(): return False p = self.head while p: print(p.data,end= ' ') p = p.next # create a singly linked list def InitList(self,data): self.head = Node (data[0]) # head node p = self.head # head pointer for i in data[1:]: node = Node(i) p.next = node p = p.next # length of singly linked list def LengthList (self): if self.IsEmpty(): return 0 p = self.head cnt = 0 while p: cnt += 1 p = p.next return cnt # Insertion of a singly linked list (insert data after the sth node ) def InsertList(self,s,data): if self.IsEmpty() or s self.LengthList(): print("Insert failed!") return p = self.head index = 1 while index self.LengthList(): print("Delete failed! ") return p = self.head index = 1 while index self.LengthList(): print("Read failed! ") return p = self.head index = 1 while index
Light-resistant design ,and support single and muilt touch points,widely use to financial telecom service,Adverstisement show,Industrial control ,public query ,self-service,E-education ,and games etc aera.Ultra-thin, ultra-narrow design, no matter whether it is external or built-in, it can adapt to various needs without affecting the appearance and saving built-in space. Infrared sensing principle, simple finishing, LED die, stable performance, high touch precision and long life.The unique installation method makes the installation of the client a breeze.The surface of the aluminum alloy is sprayed and oxidized, and the whole is delicate, simple, generous and multi-touch. Simple operation, USB connection, plug and play.
Picture show:






Diy Infrared Touch Frame,Infrared Touch Screen Kit,Install Infrared Touch Frame,Ir Touch Frame Diy,Usb Infrared Touch Screen,Outdoor Infrared Touch Screen
ShenZhen GreenTouch Technology Co.,Ltd , https://www.bbstouch.com