Although the indoor resonance mode will generate some peaks and valleys in the frequency response, it can make the resonance mode distribute more evenly at the low frequency end by selecting a reasonable ratio of the length, width and height of the room. The value is reduced to a minimum. Now take the two rooms of the same size, the length, height and width of the room as an example to see the different effects of the indoor resonance mode.
The ratio of length, height and width of the first listening room is not good. It has a length of 7.3 m, a width of 4.88 m and a height of 2.44 m. Therefore, the indoor resonance modes in terms of length, height, and width can be calculated separately as shown in Table 1.
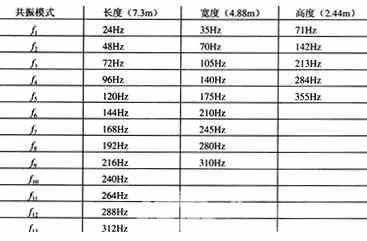
Table 1 Resonance mode in the first room
Note that the third resonance mode (f3) in length is 72 Hz, which substantially coincides with 70 Hz of the second resonance mode (f2) in width and 71 Hz of the first resonance mode (f1) in height, and these three resonance modes The coincidence will produce a very large peak at 70 Hz of the frequency response. This extremely annoying situation also occurs at 140 Hz, 213 Hz and 284 Hz, respectively. The reason why these resonance modes overlap is that the ratio of the length, width and height of the listening room is exactly a multiple. In fact, among the three resonance modes of length, width, and height, they are completely coincident at frequencies of 70.6 Hz, 141.2 Hz, and the like. Due to the rounding relationship, they are slightly opened and easy to view (Figure 1 is the relationship between these resonance modes and frequency).
Figure 1 resonance mode diagram
There is no resonance mode between 105 Hz and 140 Hz, so the stack at 140 Hz is easier to hear. As a result, a fairly loud, overweight, and heavily stained bass is heard during playback.
As seen from Fig. 1, the resonance mode is relatively close, and thus the interval left is large. The "cavity" between the resonant modes is the same as the hazard of the coincident resonant modes. They will make the adjacent resonance modes more visible.
Now let's look at the second listening room with good long, high and wide 3D dimensions. The space in this listening room is similar to the first listening room. However, the ratio of the width, height and length of the room is better. The dimensions of length, width and height are 6.4 m, 4.27 m and 3.05 m, respectively. The indoor resonance mode calculated for the first size is shown in Table 2.
Table 2 Resonance mode in the second room
The resonance pattern plotted based on the data listed in this table is shown in Figure 2.
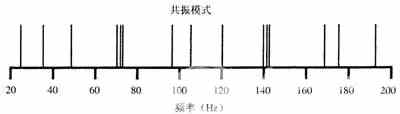
Figure 2 Resonance pattern diagram when the room ratio is good
Comparing Figure 1 with Figure 2, the resonant modes in the second listening room are more evenly distributed. Although there is still a coincidence of the resonance modes, it is no longer as serious as the first listening room. The low frequency response of the second listening room is flatter, the sound staining is also less, and the bass is more compact and powerful than the first listening room. Note that when the room is larger, the inherent resonance mode will naturally be more, so if the proportion of the room is also good, the distribution will be more uniform. The smaller the room, the worse the distribution of the indoor resonance mode.
The sloping ceiling will cause the resonance mode at the height to change, so that the resonance mode will not appear at the same frequency as the normal room, but will be pulled a little. If the low end of the ceiling is 2.4m and the high end is 3.6m, the average value of the height can be taken as 3m in the calculation. Although the sloping ceiling does not eliminate the resonance mode, it can improve the co-distribution. Similarly, the remaining walls can also tilt the resonant mode, but it does not eliminate the resonant mode.
If a square or cubic room can be avoided as a listening room, the effect of the indoor resonance mode will not be so obvious. That is to say, try not to use a room with the same width and height or the same width or length or the same length and height. Of course, rooms with equal dimensions on three sides or multiples with long sides and short sides should not be used. If the ceiling is 2.4m high, it should be avoided to have 2.4m, 4.8m and 7.2m wide or long sides. Note that the resonant mode is always present. A room with a better ratio of three sides only allows the resonance mode to be evenly distributed without blocking the coincidence of the resonance modes. Table 3 is the best ratio of rooms listed according to the degree of good or bad according to the calculation of American acoustician MMLouden.
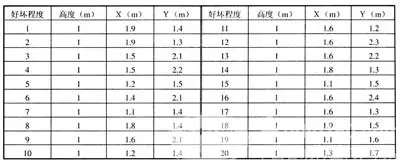
Table 3 Optimal ratio table of length, width and height of listening room
Note: The X in the table can be the length of the room, and Y can be the width, and vice versa.
According to this table, for a room with a ceiling height of 2.64 m, the ideal length and width dimensions should be 2.64 x 1.9 = 4.94 (m) and 2.64 x 1.4 = 3.64 (m), respectively. For rooms with a ceiling height of 3.8 m, the optimum length and width should be 7.3 m and 5.3 m, respectively. Note that although different values ​​can be calculated for two different height ceilings. However, the ratio of length, width and height is still the same. It is these ratios that determine how the indoor resonance mode will be distributed.
In addition, a large room with a good three-dimensional size ratio is better than a small room of the same ratio. More resonance modes are produced in large rooms, so the frequency will be closer and the distribution will naturally be more uniform. But keep in mind that a good ratio does not prevent resonance from occurring, but only allows the resonance to be evenly distributed throughout the audio band. A good ratio prevents the coincidence of the resonant modes and eliminates those intervals that affect the more severe resonant modes.
Multi-Functional Tower Socket,Black Vertical Tower Socket,2-Usb Vertical Tower Socket,4-Layers Vertical Tower Socket
Yuyao Huijun Electrical Appliance Co., Ltd. , https://www.yyhjdq.com